Question

How many moles of ZnCO3 and C6H8O7 are required to produce 30.0 mol of Zn3 (C6H5O7)2

Answer 1

To find the moles of
`ZnCO_3` and
`C_6H_8O_7` needed to produce 30.0 mol of
`Zn_3(C_6H_5O_7)^2`, one must have the balanced chemical equation to determine the stoichiometric ratios. Without the equation, it's not possible to provide an exact number of moles required. An example with photosynthesis was used to illustrate how to determine moles using stoichiometry.

To determine how many moles of
`ZnCO_3` and
`C_6H_8O_7` are required to produce 30.0 mol of
`Zn_3(C_6H_5O_7)^2`, we must use stoichiometry based on a balanced chemical equation. Unfortunately, the equation is not provided, but if we assume it is similar to the given photosynthesis equation (6
`CO_2` +
`6H_2O` →
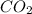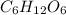`C_6H_(12)O_6`+ 6O2), we would need to know the mole-to-mole ratios from the balanced equation specific to the reaction between
`ZnCO_3` and
`C_6H_8O_7` to form
`Zn_3(C_6H_5O_7)^2`.

To assist the student with a similar example, let's consider a balanced equation that produces glucose from carbon dioxide and water during photosynthesis: 6
`CO_2` +
`6H_2O` →
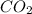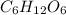`C_6H_(12)O_6`+ 6 O2. Using this equation, we can state that 6 moles of
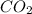`CO_2` are required to produce 1 mole of glucose (
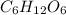`C_6H_(12)O_6`), which gives us the desired conversion factor.

For example, if a student is given 3.0 moles of
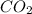`CO_2` and wants to find out how many moles of glucose (
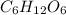`C_6H_(12)O_6`) can be produced, they can set up a proportion based on the stoichiometry of the balanced equation:

6 mol
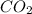`CO_2` = 1 mol
`C_6H_(12)O_6`
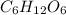
3.0 mol
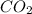`CO_2` = x mol
`C_6H_(12)O_6`

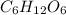
By cross-multiplying, we get: x = (1 mol
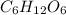`C_6H_(12)O_6`/ 6 mol
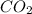`CO_2`) × 3.0 mol
`CO_2`
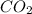
This simplifies to x = 0.5 mol
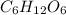`C_6H_(12)O_6`, meaning 0.5 moles of glucose are produced from 3.0 moles of
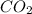`CO_2` in photosynthesis.