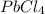The empirical formula of the compound containing lead and chlorine is
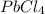, and the molecular formula is also .
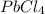
To determine the empirical formula of the compound, we need to find the ratio of the elements present in the compound.
First, let's assume we have 100 grams of the compound. Since the compound is 59.37% lead, we have 59.37 grams of lead. The remaining mass is due to chlorine.
To find the number of moles of each element, we divide the mass of each element by its molar mass.
The molar mass of lead is 207.2 g/mol, so the number of moles of lead is:
59.37 g / 207.2 g/mol = 0.286 mol
The molar mass of chlorine is 35.45 g/mol, so the number of moles of chlorine is:
(100 g - 59.37 g) / 35.45 g/mol = 1.148 mol
Next, we need to find the simplest whole number ratio between the two elements. We can do this by dividing the number of moles of each element by the smallest number of moles.
Dividing both values by 0.286, we get:
0.286 mol / 0.286 mol = 1
1.148 mol / 0.286 mol = 4
This means that the empirical formula of the compound is
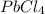, which represents one lead atom and four chlorine atoms.
To find the molecular formula, we need to know the molar mass of the compound. Given that the molar mass is 349.0 g/mol, we can calculate the empirical formula mass of
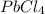as follows:
(1 atom of lead * 207.2 g/mol) + (4 atoms of chlorine * 35.45 g/mol) = 207.2 g/mol + 141.8 g/mol = 349.0 g/mol
Since the empirical formula mass matches the molar mass of the compound, the empirical formula,
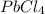, is also the molecular formula of the compound.
In conclusion, the empirical formula of the compound containing lead and chlorine is
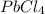, and the molecular formula is also