The average rate of change of the function f(x) on the interval 3 ≤ x ≤ 4 is equal to - 15.
How to determine the average rate of a function
In this problem we find the representation of a function on Cartesian plane, whose average rate of change must be determined by secant line formula:
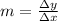
Where:
- Δx - Change in independent variable.
- Δy - Change in dependent variable.
- m - Slope
First, find the end points between 3 ≤ x ≤ 4: (3, 10), (4, - 5)
Second, determine the average rate of change on the interval given:
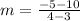
m = - 15