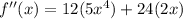Question

Find the 1st derivative and the 2nd derivative of the function.

1. f(x) = 2x^6 + 8x^3= 4x - 120

Answer 1

`f'(x) = 12x^5 + 24x^2 - 4`

`f''(x) = 60x^4 + 48x`

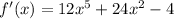
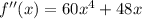
Explanation:

We can find the derivative and second derivative of the polynomial function:

`f(x) = 2x^6 + 8x^3 - 4x - 120`

using the power and sum and difference rules:

• 
  `\left[\frac{}{}x^a\frac{}{}\right]' = ax^(a-1)`
• 
  `\left[\frac{}{}f(x) + g(x)\frac{}{}\right]' = f'(x) + g'(x)`

Taking the first derivative of the function, we get:

`f'(x) = \left[\frac{}{}2x^6 + 8x^3 - 4x - 120\frac{}{}\right]'`

↓ applying the sum and difference rule

`f'(x) = \left[\frac{}{}2x^6\,\right]' + \left[\frac{}{}8x^3\,\right]' - \left[\frac{}{}4x\,\right]'- \left[\frac{}{}120\,\right]'`

↓ taking out constants

`f'(x) = 2\left[\frac{}{}x^6\,\right]' + 8\left[\frac{}{}x^3\,\right]' - 4\left[\frac{}{}x\,\right]'- \left[\frac{}{}120\,\right]'`

↓ applying the power rule

`f'(x) = 2\left[\frac{}{}6x^5\,\right] + 8\left[\frac{}{}3x^2\,\right] - 4\left[\frac{}{}1x^0\,\right] - 0`

↓ combining like terms

`\boxed{f'(x) = 12x^5 + 24x^2 - 4}`

We can repeat this process to get the second derivative:

`f''(x) = 12(5x^4) + 24(2x)`

`\boxed{f''(x) = 60x^4 + 48x}`