Question

For the polynomial below, 2 is a zero.

f(x)=x³ - 4x² + 8
Express f(x) as a product of linear factors.

Answer 1

The polynomial
`\(f(x) = x^3 - 4x^2 + 8\)` can be factored into
`\((x - 2)^2(x)\)`, with
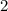`\(2\)` as a zero and
`\((x - 2)\)` as a factor repeated twice.

Given that
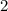`\(2\)` is a zero of the polynomial
`\(f(x) = x^3 - 4x^2 + 8\)`, it implies that
`\((x - 2)\)` is a factor of
`\(f(x)\)`. To find the other factors, we can use polynomial long division or synthetic division.

Using synthetic division, we divide
`\(f(x)\)` by
`\((x - 2)\)`:

2 | 1 -4 0 8

|_____________

| 2 -4 0

The result is
`\(1x^2 - 2x\)`, indicating that
`\(f(x)\)` can be expressed as
`\((x - 2)(x^2 - 2x)\)`. Now, we can factor the quadratic expression further:

`\[ f(x) = (x - 2)(x^2 - 2x) \]`

Factoring the quadratic term,
`\(x^2 - 2x\), we get \(x(x - 2)\)`:

`\[ f(x) = (x - 2)(x)(x - 2) \]`

Combining these factors, we express
`\(f(x)\)` as a product of linear factors:

`\[ f(x) = (x - 2)^2(x) \]`

In summary, the polynomial
`\(f(x) = x^3 - 4x^2 + 8\)` can be factored as
`\((x - 2)^2(x)\),` where
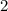`\(2\)` is a zero, and
`\((x - 2)\)` is a factor repeated twice.