Final answer:
Upon applying the chain rule to the given derivative
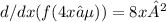 and simplifying the expression, we find that
and simplifying the expression, we find that
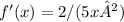 . This result is not listed among the provided multiple-choice options, indicating that there may be an error in the question as presented.
. This result is not listed among the provided multiple-choice options, indicating that there may be an error in the question as presented.
Step-by-step explanation:
To calculate
 when given that the derivative
when given that the derivative
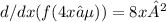 , we need to apply the chain rule. We'll call the inner function
, we need to apply the chain rule. We'll call the inner function
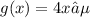 , so our outer function is
, so our outer function is
 . When applying the chain rule, we get:
. When applying the chain rule, we get:
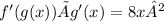
First, let's find g'(x):
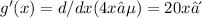
Now, let's denote
 . The given derivative becomes:
. The given derivative becomes:
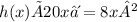
To find
 , we divide both sides by
, we divide both sides by
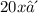 :
:
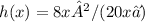
 simplifies to:
simplifies to:
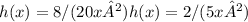
Recall that
 represents
represents
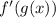 , and since
, and since
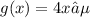 , we replace
, we replace
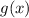 with
with
 to find
to find
 :
:
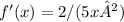
The correct answer is not in the options provided since there seems to be an error.
 simplifies to
simplifies to
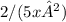 and not to any of the options given (a, b, c, d). So,
and not to any of the options given (a, b, c, d). So,
 is the correct derivative function of
is the correct derivative function of
 .
.