Question

If f(x) = cot(x) and f(a) = 6, find the exact value of a:

a) π/6
b) π/4
c) π/3
d) π/2

Answer 1

None of the given options for angle a, when
`f(x) = cot(x)` and
`f(a) = 6`, correspond to a cotangent value of
`6`. The value of
`tan(a)`would be
`1/6`, which does not match any of the well-known angles provided.

Step-by-step explanation:

To find the exact value of a when
`f(x) = cot(x) and f(a) = 6` we must look for an angle where the cotangent is equal to 6. Cotangent is defined as the ratio of the adjacent side to the opposite side in a right-angled triangle or equivalently the reciprocal of the tangent function. Since cotangent values are the same as tangent values for angles in different quadrants, we must consider this when looking for a.

First, let's rewrite the cotangent in terms of sine and cosine to find the corresponding tangent value:

`cot(x) = 1 / tan(x) = cos(x) / sin(x)`

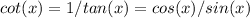
Since
`cot(a) = 6`, this implies:

`1 / tan(a) = 6 tan(a) = 1 / 6`

This ratio does not correspond to any of the well-known angles where tangent values can be determined exactly (such
`as π/6, π/4, or π/3` ). However, we can approximate that if is positive and less than 1, then angle a must be in the first quadrant because tangent is positive in the first and third quadrants, but
`1/6` is not a typical third quadrant ratio.

Therefore, without the specific value for a, we cannot precisely identify angle a from the given options
`(a) π/6, (b) π/4, (c) π/3, or (d) π/2`. Each of these options has a known tangent value that does not match 1/6. So, none of these options are the correct value for a.