Question

The function f(t)=-16t^2+46t+18 represents the height in feet of a pumpkin t seconds after it is launched from a catapult five feet from the ground.

after how many seconds does the pumpkin land on the ground? Round to the nearest 10th if necessary

Answer 1

The pumpkin lands on the ground approximately 3.98 seconds after it is launched from the catapult. Rounding to the nearest tenth, the pumpkin lands on the ground after approximately 4 seconds.

To find the time it takes for the pumpkin to land on the ground, we need to determine when the height, represented by the function f(t), becomes zero.

The given function is f(t) = -16
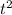`t^2` + 46t + 18, where t represents the time in seconds and f(t) represents the height in feet.

To find when the pumpkin lands on the ground, we set f(t) equal to zero and solve for t:

-16
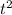`t^2` + 46t + 18 = 0

To solve this quadratic equation, we can either factor it or use the quadratic formula. In this case, factoring is not straightforward, so let's use the quadratic formula:

t = (-b ±
`√((b^2 - 4ac))`) / (2a)

In our equation, a = -16, b = 46, and c = 18. Substituting these values into the formula:

t = (-46 ±
`√((46^2 - 4(-16)(18))))` / (2(-16))

Simplifying further:

t = (-46 ±
`√((2116 + 1152)))` / (-32)

t = (-46 ± √
`√(3268)`) / (-32)

Now, we need to find the two possible solutions for t by evaluating both the positive and negative square root of 3268:

t = (-46 +
`√(3268)`) / (-32) ≈ 3.98 seconds

t = (-46 -
`√(3268)`) / (-32) ≈ -0.11 seconds

Since time cannot be negative in this context, we discard the negative solution.

Therefore, the pumpkin lands on the ground approximately 3.98 seconds after it is launched from the catapult. Rounding to the nearest tenth, the pumpkin lands on the ground after approximately 4 seconds.