Question

A 60 kg acrobat is in the middle of a 10 m long tightrope. The center of the rope dropped 30 cm in relation to the ends that are attached to fixed supports. What is the tension in each half of the rope?

Answer 1

The tension in each half of the rope, is approximately 4,908.8 N

Step-by-step explanation:

The mass of the acrobat, m = 60 kg

The length of the rope, l = 10 m

The extent by which the center dropped = 30 cm = 0.3 m

Let, 'T' represent the tension in each half of the rope

Weight, W = Mass, m × The acceleration due to gravity, g

∴ W = m × g

The acceleration due to gravity, g ≈ 9.8 m/s²

∴ The weight of the acrobat, W = 60 kg × 9.8 m/s² ≈ 588 N

The angle the dropped rope makes with the horizontal, θ is given as follows;

θ = arctan((0.3 m)/(5 m)) = arctan(0.06) ≈ 3.434°

At equilibrium, the sum of vertical forces,
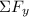`\Sigma F_y` = 0

The vertical component of the tension,
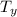`T_y`, in each half of the rope is given as follows;

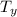`T_y` = T × sin(θ)

∴
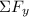`\Sigma F_y` = W + T × sin(θ) + T × sin(θ) = W + 2 × T × sin(θ)

Plugging in the values, with θ = arctan(0.06) for accuracy, we get;

588 N + 2 × T × sin(arctan(0.06) = 0

∴ 2 × -T × sin(arctan(0.06) = 588 N

-T= 588 N/(2 × sin(arctan(0.06)) = 4,908.81208 N ≈ 4,908.8 N

The tension in each half of the rope, T ≈ 4,908.8 N.