Question

For which value of x does each expression make sense

Answer 1

The values of x for which each expression make sense are

• 
  `\sqrt{|x| + 1`: All values of x
• 
  `√((-2x)^2)`: All values of x
• 
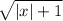  `√(-125x^3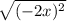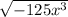)`: All values of x not more than 0
• 
  `√(13-(13 - 2x))`: All nonnegative values of x

For which value of x does each expression make sense

From the question, we have the following parameters that can be used in our computation:

`\sqrt{|x| + 1`

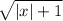
For the expression to make sense, it must be at least 0

So, we have

`√(|x| + 1) \ge 0`

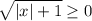
Square both sides

`\ge 0`

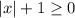
This gives

`x \ge -1`

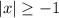
All absolute values are greater than -1

So, the expression make sense for all values of x

Next, we have

`√((-2x)^2)`

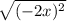
Evaluate the square root

-2x

So, the expression make sense for all values of x

Next, we have

`√((-5x)^3)`

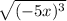
Expand

`√(-125x^3)`

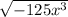
For the expression to make sense, it must be at least 0

So, we have

`√(-125x^3) \ge 0`

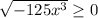
This gives

`-125x^3 \ge 0`

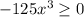
Divide

`x^3 \le 0`

Evaluate

`x \le 0`

So, the expression makes sense for all values of x not more than 0

Lastly, we have

`√(13-(13 - 2x))`

Expand and evaluate

`√(2x)`

This expression will makes for all nonnegative values of x