Question

Need help with this question

Answer 1

The equation of the parabola in vertex form is
`(y^2)/(4) - (x^2)/(4) = 1`.

How to derive the equation of a hyperbola

According to the figure, a hyperbola with major axis parallel with y-axis is shown. The vertex form of the hyperbola is shown below:

`((y - k)^2)/(a^2)-((x-h)^2)/(b^2) = 1`

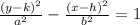
Where:

• (h, k) - Coordinates of the vertex.
• a - Length of the major axis.
• b - Length of the minor axis.

And the asymptote equations are, respectively:

`y = \pm (a)/(b) \cdot x`

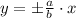
Then, the equation of the hyperbola is simplified:

y² - x² = a²

Finally, we find the length of the major axis based on the location of any of the two co-vertices:

4² - 0² = a²

a² = 4²

a = 2

And the equation of the hyperbola in vertex form is:

`(y^2)/(4) - (x^2)/(4) = 1`