Question

A campsite charges $16 per day for the site rental and $12 for parking. The total campsite charge x (in dollars) is given by x = 16y + 12 where y is the number of days that the site is rented. Calculate the x and y intercepts.

Answer 1

`\sf x-intercept = (12, 0)`

`\sf y-intercept = (0,-(3)/(4) )`

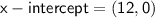
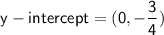
Explanation:

Let's calculate the x and y intercepts for the given equation
`\sf x = 16y + 12`, where:

• 
  `\sf x` represents the total campsite charge in dollars.
• 
  `\sf y` represents the number of days the site is rented.

X-Intercept:

The x-intercept occurs when the number of days rented (
`\sf y`) is 0. Setting
`\sf y = 0` in the equation and solving for
`\sf x`:

`\sf x = 16(0) + 12`

`\sf x = 0 + 12`

`\sf x = 12`

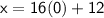
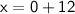
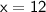
Therefore, the x-intercept is
`\sf (12, 0)`. This means that even if the site is not rented for any days, the total campsite charge will still be $12 due to the parking fee.

Y-Intercept:

The y-intercept occurs when the total campsite charge (
`\sf x`) is 0.

Setting
`\sf x = 0` in the equation and solving for
`\sf y`:

`\sf 0 = 16y + 12`

`\sf -12 = 16y`

`\sf y = -(12)/(16)`

`\sf y = -(3)/(4)`

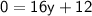
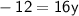
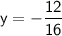
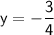
However, the number of days rented cannot be negative, so this solution is not realistic in the context of the problem. Therefore, there is no real y-intercept in this case. Although we can say that:
`\sf y-intercept = (0,-(3)/(4) )`

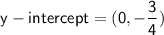
In summary:

-The x-intercept is
`\sf (12, 0)`.

-There is no real y-intercept in this context.