Question

Find a line that lies entirely in the set defined by the equation _______.

a) y = mx + b
b) Ax + By = C
c) Quadratic formula
d) Polar coordinates equation

Answer 1

A line that lies entirely in a set defined by an equation is likely represented by a linear equation. The most common form is
`y = mx + b` , where m is the slope and b is the y-intercept.
`Ax + By = C` is also a linear form but quadratic formulas and polar coordinates do not represent lines.

Step-by-step explanation:

When searching to find a line that lies entirely in the set defined by the equation, we can examine several types of equations. The set in question is most likely defined by a linear equation, as linear equations define straight lines in a coordinate system. The most common form of a linear equation is
`y = mx + b` , where m is the slope of the line and b is the y-intercept. Slope is defined as the ratio of the change in y to the change in x (rise over run), and the y-intercept is where the line crosses the y-axis. The equation
`Ax + By = C` is another form of a linear equation and can be rearranged to the slope-intercept form by solving for y.

However the quadratic formula is not used to define a line, as it pertains to quadratic equations, which represent parabolas not lines. Likewise polar coordinates equations describe curves in a polar coordinate system, not the straight lines as defined by linear equations. A specific example of a linear equation is
`y = 3x + 9`, where the slope (m) is
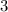`3`, and the y-intercept (b) is
`9`. This can be used to demonstrate that by defining a slope and a y-intercept, one can identify a specific straight line that fits in the given set.