The LHS is equal to the RHS, and the trigonometric identity is proved:
![\[ \tan(x) + \cot(x) = \sec(x) \csc(x) \]](https://img.qammunity.org/2024/formulas/mathematics/college/5tjwxbikcom3flhwm726ccbbeohzjq2i7f.png)
To prove the trigonometric identity
 we'll start with the left-hand side (LHS) and manipulate it to match the right-hand side (RHS).
we'll start with the left-hand side (LHS) and manipulate it to match the right-hand side (RHS).
Starting with the LHS:
![\[ \tan(x) + \cot(x) \]](https://img.qammunity.org/2024/formulas/mathematics/college/wfkr6phsqpflonoh62wk36tsn8sh5rpl03.png)
We know that
 and
and
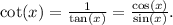
Now, substitute these expressions into the LHS:
![\[ (\sin(x))/(\cos(x)) + (\cos(x))/(\sin(x)) \]](https://img.qammunity.org/2024/formulas/mathematics/college/slyir6xcz5w10egtvwp87t0u9akx6945bv.png)
To combine these fractions, find a common denominator, which is the product of the denominators
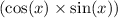
![\[ (\sin^2(x) + \cos^2(x))/(\cos(x) \sin(x)) \]](https://img.qammunity.org/2024/formulas/mathematics/college/mnt4sxvgis3egdfr9v7matu72id4ym7pd2.png)
Recall that
 so the expression becomes:
so the expression becomes:
![\[ (1)/(\cos(x) \sin(x)) \]](https://img.qammunity.org/2024/formulas/mathematics/college/jdvyaykbhqotfn4zhpi6exzbmwtgwy71yh.png)
Now, express
 :
:
![\[ (1)/(\cos(x) \sin(x)) = (1)/(\cos(x)) \cdot (1)/(\sin(x)) = \sec(x) \csc(x) \]](https://img.qammunity.org/2024/formulas/mathematics/college/u9lkdzm22mdxto1vi46ps3oo4zbtjrbkqa.png)
Therefore, we've shown that the LHS is equal to the RHS, and the trigonometric identity is proved:
![\[ \tan(x) + \cot(x) = \sec(x) \csc(x) \]](https://img.qammunity.org/2024/formulas/mathematics/college/5tjwxbikcom3flhwm726ccbbeohzjq2i7f.png)