A statement that correctly describes whether ΔJKL is a right triangle is: C. ΔJKL is not a right triangle because no two of its sides are perpendicular.
In Mathematics and Geometry, the slope of any straight line can be determined by using the following mathematical equation;
Slope (m) = (Change in y-axis, Δy)/(Change in x-axis, Δx)
Slope (m) = rise/run
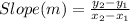
By substituting the given data points J (−5, -1) and L (2, -5) into the formula for the slope of a line, we have;
Slope (m) of JL = (-5 + 1)/(2 + 5)
Slope (m) of JL = -6/7
Slope (m) of JK = (1 + 1)/(0 + 5)
Slope (m) of JK = 2/5
Slope (m) of KL = (-5 - 1)/(2 - 0)
Slope (m) of KL = -6/2
Slope (m) of KL = -3
Since none of the slopes are negative reciprocals of each other, we can logically deduce that ΔJKL is not a right triangle because no two of its sides are perpendicular.