The probability that the top four finishers are all from the same team is
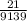, which is the simplest form of the fraction.
How to calculate the probability
To calculate the probability that the top four finishers are all from the same team, find the number of favorable outcomes (where all four finishers are from the same team) and divide it by the total number of possible outcomes.
In this case, there are 10 athletes on the same team and 40 athletes in total. We want to calculate the probability of selecting 4 athletes from the team of 10.
The number of favorable outcomes is given by the permutation formula:
10P4 = (10!)/(10-4)! = (10!)/(6!) = (10 * 9 * 8 * 7)/(4 * 3 * 2 * 1) = 5,040/24 = 210
The total number of possible outcomes is given by the permutation formula for selecting 4 athletes from a group of 40:
40P4 = (40!)/(40-4)! = (40!)/(36!) = (40 * 39 * 38 * 37)/(4 * 3 * 2 * 1) = 91,390
Therefore, the probability that the top four finishers are all from the same team is:
10P4/40P4 = 210/91,390
To simplify this fraction, divide both the numerator and denominator by their greatest common divisor (GCD), which in this case is 10:
210/91,390 = (210/10)/(91,390/10) =
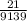
So, the probability that the top four finishers are all from the same team is
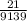, which is the simplest form of the fraction.
In a cross country race of 40 athletes, 10 of them are on the same team. The probability that the top four finishers are all from that same team is given as
10P4/40P4
Express your answer as a fraction in simplest form, Provide your answer below