Question

Use the diagram for questions 2 – 4.

Answer 1

2. m∠B = 112.63°, mLADB = 112.63°.

3. AE ≈ √205.

4. BC ≈ √133 (rounded to nearest hundredths).

2. To find m∠B, we can use the fact that the sum of angles in a triangle is 180 degrees. Since ∠BCA and ∠CAB are complementary angles, we can subtract mBC from 180 degrees to find m∠B.

m∠B = 180° - mBC

m∠B = 180° - 67.37°

m∠B = 112.63°

To find mLADB, we can use the fact that angles on a straight line add up to 180 degrees. Since ∠BCA and ∠CAB are supplementary angles, we can subtract mBC from 180 degrees to find mLADB.

mLADB = 180° - mBC

mLADB = 180° - 67.37°

mLADB = 112.63°

Therefore, m∠B = 112.63° and mLADB = 112.63°.

3. Since BE = DE and AC = 13, we can use the Pythagorean Theorem to find AE. The Pythagorean Theorem states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.

`AE^2 = BE^2 + AB^2`

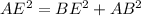
Substituting the given values:

`AE^2 = 6^2 + 13^2`

`AE^2 = 36 + 169`

`AE^2 = 205`

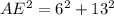
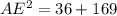
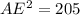
Taking the square root of both sides:

AE = √205

Therefore, AE is approximately equal to √205.

4. To find BC, we can use the fact that AC is the hypotenuse of a right triangle and BC is one of the legs. We can use the Pythagorean Theorem to solve for BC.

`AC^2 = BC^2 + AB^2`

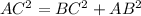
Substituting the given values:

`13^2 = BC^2 + 6^2`

`169 = BC^2 + 36`

`BC^2 = 169 - 36`

`BC^2 = 133`

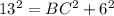
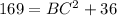
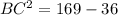
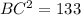
Taking the square root of both sides:

BC = √133

Therefore, BC is approximately equal to √133, rounded to the nearest hundredths place.