Question

Please help me solve for the expectation and the variance.

Answer 1

The expectation E(X) of X is 20.

The variance Var(X) of X is 180.

How to find the expectation E(X) of X

(a) To find the expectation E(X) of X, calculate the weighted average of the values of X using their respective probabilities.

E(X) = (0 * P(X=0)) + (10 * P(X=10)) + (20 * P(X=20)) + (30 * P(X=30)) + (40 * P(X=40))

E(X) = (0 * 0.15) + (10 * 0.30) + (20 * 0.10) + (30 * 0.30) + (40 * 0.15)

E(X) = 0 + 3 + 2 + 9 + 6

E(X) = 20

Therefore, the expectation E(X) of X is 20.

(b) To find the variance Var(X) of X, first calculate the squared deviations from the mean (E(X)).

Squared Deviations:

`(0 - 20)^2 = 400\\(10 - 20)^2 = 100\\(20 - 20)^2 = 0\\(30 - 20)^2 = 100\\(40 - 20)^2 = 400`

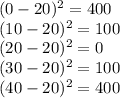
Next, multiply each squared deviation by its respective probability and sum them up:

Var(X) = (400 * 0.15) + (100 * 0.30) + (0 * 0.10) + (100 * 0.30) + (400 * 0.15)

Var(X) = 60 + 30 + 0 + 30 + 60

Var(X) = 180

Therefore, the variance Var(X) of X is 180.