Question

Which of the coordinate pairs is a point on the line y = -2/5x + 4?

A.) (2, 3)
B.) (-5, 6)
C.) (6, 2)
D.) (-2/5, 4)​

Answer 1

its D you don't even need to do all the work bc the same numbers are right there in the equation

Answer 2

B.) (-5, 6)

Explanation:

to solve algebraically, test the coordinate pairs in the equation
`y = -(2)/(5)x + 4`

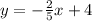
to solve graphically, enter the equation
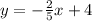`y = -(2)/(5)x + 4` into a graphing calculator and graph the coordinate pairs as well to see which one is on the line.

(2, 3) is NOT a solution.

steps for solving algebraically:

first, identify the x and y values in your coordinate pair.

• 2 is the x-value and 3 is the y-value. coordinate pairs are always written as (x, y).

plug in 2 for x in
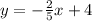`y = -(2)/(5)x + 4` (it doesn't matter if you plug in x or y first, i personally always start with the x-value but it really doesn't matter what order you do it in.)

• y = -2/5x + 4 ⇒ y = -2/5(2) + 4

now plug in 3 for y.

• y = -2/5(2) + 4 ⇒ 3 = -2/5(2) + 4

your equation is now 3 = -2/5(2) + 4. begin simplifying by multiplying -2/5 and 2.

• 3 = -2/5(2) + 4 ⇒ 3 = -0.8 + 4 (i converted my answer to a decimal because i'm better at dealing with decimals as opposed to fractions lol)

now add -0.8 + 4 to simplify the rest of the right side of the equation.

• 3 = -0.8 + 4 ⇒ 3 = 3.2

3 and 3.2 are not equal, therefore (2, 3) is not a solution.

(-5, 6) IS a solution.

steps for solving algebraically:

first, identify the x and y values in your coordinate pair.

• -5 is the x-value and 6 is the y-value. coordinate pairs are always written as (x, y).

plug in -5 for x in
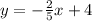`y = -(2)/(5)x + 4` (it doesn't matter if you plug in x or y first, i personally always start with the x-value but it really doesn't matter what order you do it in.)

• y = -2/5x + 4 ⇒ y = -2/5(-5) + 4

now plug in 6 for y.

• y = -2/5(-5) + 4 ⇒ 6 = -2/5(-5) + 4

your equation is now 6 = -2/5(-5) + 4. begin simplifying by multiplying -2/5 and -5.

• 6 = -2/5(-5) + 4 ⇒ 6 = 2 + 4

now add 2 + 4 to simplify the rest of the right side of the equation.

• 6 = 2 + 4 ⇒ 6 = 6

6 and 6 are equal, therefore (-5, 6) is a solution.

although we have identified (-5, 6) as a solution, i'm still going to check the rest of the points just to be sure! :)

(6, 2) is NOT a solution.

steps for solving algebraically:

first, identify the x and y values in your coordinate pair.

• 6 is the x-value and 2 is the y-value. coordinate pairs are always written as (x, y).

plug in 6 for x in
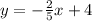`y = -(2)/(5)x + 4` (it doesn't matter if you plug in x or y first, i personally always start with the x-value but it really doesn't matter what order you do it in.)

• y = -2/5x + 4 ⇒ y = -2/5(6) + 4

now plug in 2 for y.

• y = -2/5(2) + 4 ⇒ 2 = -2/5(2) + 4

your equation is now 2 = -2/5(6) + 4. begin simplifying by multiplying -2/5 and 6.

• 2 = -2/5(6) + 4 ⇒ 2 = -2.4 + 4 (i converted my answer to a decimal because i'm better at dealing with decimals as opposed to fractions lol)

now add -2.4 + 4 to simplify the rest of the right side of the equation.

• 2 = -2.4 + 4 ⇒ 2 = 1.6

2 and 1.6 are not equal, therefore (6, 2) is not a solution.

(-2/5, 4) is NOT a solution.

i see that they want to trick you with this one by using the values that are in other spots in the equation... that's crafty

steps for solving algebraically:

first, identify the x and y values in your coordinate pair.

• -2/5 is the x-value and 4 is the y-value. coordinate pairs are always written as (x, y).

plug in -2/5 for x in
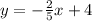`y = -(2)/(5)x + 4` (it doesn't matter if you plug in x or y first, i personally always start with the x-value but it really doesn't matter what order you do it in.)

• y = -2/5x + 4 ⇒ y = -2/5(-2/5) + 4

now plug in 4 for y.

• y = -2/5(-2/5) + 4 ⇒ 4 = -2/5(-2/5) + 4

your equation is now 4 = -2/5(-2/5) + 4. begin simplifying by multiplying -2/5 and -2/5.

• 4 = -2/5(-2/5) + 4 ⇒ 4 = 0.16 + 4 (i converted my answer to a decimal because i'm better at dealing with decimals as opposed to fractions lol)

now add 0.16 + 4 to simplify the rest of the right side of the equation.

• 4 = 0.16 + 4 ⇒ 4 = 4.16

4 and 4.16 are not equal, therefore (-2/5, 4) is not a solution.

as for finding the solution on a graph, enter the equation for the line as well as the coordinate pairs into a graphing calculator. here i used a handy little site called desmos in order to graph all of this. the first photo i attached contains what i entered into the calculator, and the second photo i attached shows the graph. as you can see, the only point that is actually on the line is (-5, 6), which is why (-5, 6) is a solution to
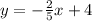`y = -(2)/(5)x + 4` , and the other coordinate pairs are not solutions to that equation because they are not on the line.

i hope this helps! have a lovely rest of your day <3