Question

What is the slope of a line that is perpendicular to the line
y = 2x – 6?

Answer 1

The slope of a line that is perpendicular to the line y = 2x – 6 is -1/2.

Explanation:

The slope-intercept form of the line equation

`y = mx+b`

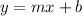
where

• 
  `m` is the slope

• 
  `b` is the y-intercept

Step 1:

Finding the slope of the given equation

The given equation is

`y = 2x - 6`

comparing with the slope-intercept form of the line equation

The slope of the equation is: m = 2

Step 2:

Determining the slope of the perpendicular line

In Mathematics, a line perpendicular to another line has a slope that is the negative reciprocal of the slope of the other line.

• As the slope of the equation is: m = 2

Therefore, the slope of the new perpendicular line:

`-(1)/(m)=-(1)/(2)`

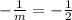
Hence, the slope of a line that is perpendicular to the line y = 2x – 6 is -1/2.

Important Tip:

• The product of the slopes of perpendicular lines is -1.

Verification:

The slope of the given line:

`m_1=2`

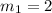
The slope of the perpendicular line:

`m_2=-(1)/(2)\:\:\:\:`

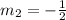
The product of the slopes is:

`\:m_1* \:m_2\:=2* -(1)/(2)\:\:=-1`

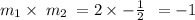
As the product of the slopes of perpendicular lines is -1, therefore, the lines are perpendicular.

Thus, the slope of a line that is perpendicular to the line y = 2x – 6 is -1/2.