Question

Determine the cofactor of a32 in the matrix
4 -2 0
A= 6 7 0
4 8 6

Answer 1

The cofactor of the element at a32 in the given matrix is
`\(-24\)`

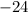
To determine the cofactor of the element at position a32 in the matrix A:

`\[ A = \begin{bmatrix} 4 & -2 & 0 \\ 6 & 7 & 0 \\ 4 & 8 & 6 \end{bmatrix} \]`

The cofactor of an element in a matrix is calculated using the following formula:

`\[ C_(ij) = (-1)^(i+j) * M_(ij) \]`

where
`\( C_(ij) \)` is the cofactor,
`\( i \)` is the row number,
`\( j \)` is the column number, and
`\( M_(ij) \)` is the determinant of the matrix obtained by deleting the
`\( i \)`-th row and
`\( j \)`-th column.

In this case,
`\( a32 \)` corresponds to the element in the 3rd row and 2nd column. So,
`\( i = 3 \) and \( j = 2 \)`.

`\[ C_(32) = (-1)^(3+2) * M_(32) \]`

Now, let's find
`\( M_(32) \)`, which is the determinant of the matrix obtained by deleting the 3rd row and 2nd column:

`\[ M_(32) = \text{det} \left( \begin{bmatrix} 4 & 0 \\ 6 & 6 \end{bmatrix} \right) \]`

`\[ M_(32) = (4 * 6) - (0 * 6) = 24 \]`

Now, substitute this into the cofactor formula:

`\[ C_(32) = (-1)^(3+2) * 24 = -24 \]`

So, the cofactor of the element at a32 in the given matrix is
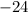`\(-24\)`.