Question

PLS Help While on a strenuous hike, Tara recorded her distance from the peak of the mountain at two different time intervals. The table shows the two pieces of data she collected.

Answer 1

Explanation:

Equation of a line representing the relation between distance from the peak of the mountain and time is,

h = mt + b

Here, m = Slope of the line

b = y-intercept

Since, slope of the line passing through two points
`(x_1,y_1)` and
`(x_2,y_2)` is given by,

m =
`(y_2-y_1)/(x_2-x_1)`

From the table attached,

Slope of the line passing through (2, 2600) and (5, 950) will be,

m =
`(2600-950)/(2-5)`

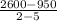
= -550

Therefore, equation of the line will be,

h = -550t + b

Since, point (2, 2600) lies on this line,

2600 = -550(2) + b

b = 2600 + 1100

b = 3700

So, equation of the line will be,

h = -550t + 3700

Input - output values for this line,

t 2 4 6

h 2600 1500 400

Now we can plot these points and get the graph of the line.