Question

The concentration of a certain drug, in mg/L, can be modeled by the following function: C(t)= 5t *e^-0.8t , where t is the number of hours after the drug was administered. The drug is effective if its concentration is greater than 1.2 mg/L. Use the graph of the function to determine the interval of time when the drug is effective.

Answer 1

The interval of time when the drug is effective. is t ≥ 0

How to determine the interval of time when the drug is effective.

From the question, we have the following parameters that can be used in our computation:

`\text{f(t)}= 5t * e^(0.8 t)`

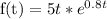
First, we plot the graph of the function f(t)

See attachment for the graph

The negative values of t on the x-axis cannot be considered

This is so because time cannot be negative

Considering t ≥ 0, we have that

As the value of t increase, the function value increases

This means that the drug is effective for all non-negative values of t

Hence, the interval of time when the drug is effective. is t ≥ 0