Question

Solve 64^(2x 4)=16^(5x)

Answer 1

The solution for the equation
`64^(2x + 4) = 16^(5x)` is x = 3.

How to solve the equation?

Here we want to solve the equation:

`64^(2x + 4) = 16^(5x)`

We can see that the variables are in the exponents, to take them down, we need to apply a logarithm in both sides of the equation. We can apply the natural logarithm in both sides so we get:

`ln(64^(2x + 4)) = ln(16^(5x))\\\\(2x + 4)*ln(64) = 5x*ln(16)`

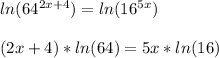
Now we can solve this for x:

4*ln(64) = 5x*ln(16) - 2x*ln(64)

4*ln(64) = x*(5*ln(16) - 2*ln(64))

x = 4*ln(64)/(5*ln(16) - 2*ln(64))

x = 3