Answer:
16 years
Explanation:
Given
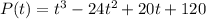
Required
Year they made loss
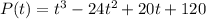
Start by differentiating P w.r.t t
Using first principle:

Equate to 0, in order to solve for t

So, we have:
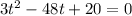
Solve using quadratic equation
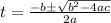
Where
a = 3, b = -48 and c = 20
So, we have:
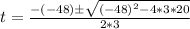

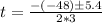

Split:
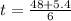 or
or

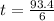 or
or
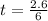
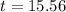 or
or
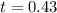
Approximate to whole numbers
 or
or
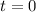
Hence, they made loss 16 years after they took over