1 Answer

Apardes · Answer 1 · 2024-09-16T23:15:35+0000

The arc length of the circular sector is equal to
$(14\pi)/(9)$ square units.

How to compute the arc length of a circular sector

In this problem we find the representation of a circular sector, whose arc length can be found by means of the following equation:

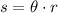
$s = \theta \cdot r$

Where:

And the central angle is:

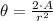
$\theta = (2\cdot A)/(r^2)$

Where A is the area of the circular sector.

Please notice that 2π radians equals 360º and a complete revolutions means a central angle measure of 2π radians.

If we know that
$A = (14\pi)/(9)$ and r = 2, then the area of the circular sector is the following:

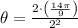
$\theta = (2\cdot \left((14\pi)/(9) \right))/(2^2)$

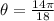
$\theta = (14\pi)/(18)$

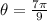
$\theta = (7\pi)/(9)$

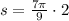
$s = (7\pi)/(9)\cdot 2$

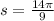
$s = (14\pi)/(9)$

The arc length of the circular sector is equal to
$(14\pi)/(9)$ square units.

Please log in or register to add a comment.