Question

In a 30°-60°-90° right triangle, the measure of the hypotenuse is twice the measure of the short leg, and the measure of the longer leg is the measure of the short leg times √3.

A) True
B) False

Answer 1

The statement about the side lengths of a
`30°-60°-90°` right triangle is True, as the sides follow a specific ratio according to the Pythagorean theorem.

Step-by-step explanation:

The statement, In a
`30°-60°-90°` right triangle, the measure of the hypotenuse is twice the measure of the short leg, and the measure of the longer leg is the measure of the short leg times
`√3`, is indeed True. In such a triangle, the sides have a unique ratio. If the length of the short leg (opposite the
`30° angle`) is represented by a, then the length of the hypotenuse (opposite the
`90° angle`) is
`2a`, and the length of the longer leg (opposite the
`60° angle`) can be expressed as
`a√3.`

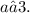
This is consistent with the properties of a
`30°-60°-90°` triangle and can be derived from the Pythagorean theorem,
`a² + b² = c²`, where c would be the hypotenuse and a and b would be the two legs of the right triangle.