Final answer:
The total amount of kinetic energy in the system before and after the collision is 875 J. The final velocities of the balls assuming a completely elastic collision are 6.67 m/s and 10 m/s, respectively.
Step-by-step explanation:
In order to find the total amount of kinetic energy in the system before and after the collision, we need to use the formula for kinetic energy:
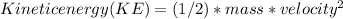
Before the collision, the first ball has a mass of 15kg and a velocity of 10m/s, so its kinetic energy is:
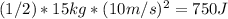
The second ball has a mass of 10kg and a velocity of -5m/s, so its kinetic energy is:
(negative sign indicates direction)
The total kinetic energy before the collision is the sum of the two: 750 J + 125 J = 875 J
In an elastic collision, kinetic energy is conserved. Since the masses of the balls remain the same, the total kinetic energy after the collision will also be 875 J.
To find the final velocities of both balls, we can use the conservation of momentum:
Momentum before collision = Momentum after collision
The momentum of an object is given by:
Momentum (p) = mass * velocity
Before the collision, the momentum of the first ball is 15kg * 10m/s = 150 kg·m/s, and the momentum of the second ball is 10kg * -5m/s = -50 kg·m/s (negative sign indicates direction).
After the collision, the momentum of the first ball will be:
Final momentum = 150 kg·m/s - 50 kg·m/s = 100 kg·m/s
To find the final velocity, we divide the final momentum by the mass of the ball:
Final velocity = 100 kg·m/s / 15kg = 6.67 m/s
The final velocity of the second ball will be:
Final velocity = 100 kg·m/s / 10kg = 10 m/s
Therefore, the final velocities of the balls after the completely elastic collision are 6.67 m/s and 10 m/s, respectively.