Question

4. The diagram below shows a crescent formed by two circles of radii 3cm and 5cm centres A and B respectively. B 5cm 60° A C 3cm D Calculate the area of the shaded region if it subtends an angle of 60° at centre B. (10 mks)​

Answer 1

The area of the shaded region is approximately 2.09 square centimeters.

The area of the shaded region can be found by calculating the area of the sector of the larger circle centered at B with central angle 60° and subtracting the area of the smaller circle.

Here's how to do it:

1. Calculate the area of the sector of the larger circle:

The area of a sector is given by the formula
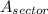`A_{sector` = (θ/360°) * πr², where `θ` is the central angle in degrees and r is the radius of the circle.

In this case, θ = 60° and r = 5 cm. Substituting these values into the formula, we get:

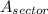`A_{sector` = (60°/360°) * π(5 cm)² = π/6 * 25π cm² = 25π/6 cm²

2. Calculate the area of the smaller circle:

The area of a circle is given by the formula πr², where r is the radius of the circle.

In this case, r = 3 cm. Substituting this value into the formula, we get:

`A_{circle` = π(3 cm)² = 9π cm²

3. Calculate the area of the shaded region:

Finally, subtract the area of the smaller circle from the area of the sector to get the area of the shaded region:

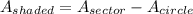`A_(shaded) = A_(sector) - A_(circle)` = 25π/6 cm² - 9π cm² ≈ 2.09 cm²

Therefore, the area of the shaded region is approximately 2.09 square centimeters.