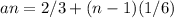Question

The sixth term of an arithmetic sequence is 3/2, and the twelfth term is 5/2.

1) What is the common difference of the arithmetic sequence?
2) What is the explicit rule for the arithmetic sequence?

Answer 1

The common difference of the arithmetic sequence is
`1/6` and the explicit rule is
`an = 2/3 + (n - 1)(1/6).`

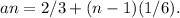
Step-by-step explanation:

To solve this question, we'll first find the common difference, and then create an explicit rule for the arithmetic sequence.

Common Difference

We know that the sixth term a6 of the sequence is
`3/2`, and the twelfth term
`a12 is 5/2.` The common difference d can be found using the formula for the nth term of an arithmetic sequence, which is
`an = a1 + (n - 1)d`. We can set up an equation by subtracting a6 from a12 to find the common difference over six terms:

`a12 - a6 = 6d`

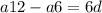
Substituting the given values:

`(5/2) - (3/2) = 6d`

`1 = 6dd = 1/6`

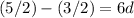
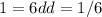
Explicit Rule:

To find the explicit rule, we also need the first term a1. We already found d, so we can rearrange the nth term formula to solve for a1 using the sixth term:

`3/2 = a1 + 5(1/6)`

`3/2 = a1 + 5/6`

`a1 = 3/2 - 5/6 = 9/6 - 5/6`

`a1 = 4/6 = 2/3`

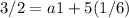
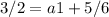
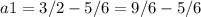
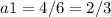
Now that we have a1, we can write the explicit formula as:

`an = 2/3 + (n - 1)(1/6)`