Final answer:
To perform a t-test for the claim that
with
we use the sample mean (xbar), standard deviation (s), and sample size (n) to calculate the t-statistic. The P-value is then determined from a t-distribution table or statistical software for a two-tailed test, comparing it against the critical value to decide on the null hypothesis.
Step-by-step explanation:
In order to test the claim about the population mean μ, we use a t-test since the population standard deviation is unknown and the sample size is small
The claim is that
with a level of significance
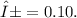
The formula for the t-test statistic
where xbar is the sample mean, μ is the hypothesized population mean, s is the sample standard deviation, and n is the sample size. Using the provided sample statistics:
we calculate the t-statistic:
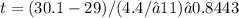
To calculate the P-value for this t-statistic, we would refer to a t-distribution table or use statistical software with two-tailed test since our claim is
. However, without the exact P-value provided here, one would typically compare the calculated t-statistic with critical t-values from the t-distribution table corresponding to degrees of freedom
and the given level of significance
. If the absolute value of the calculated t-statistic is greater than the critical value, the null hypothesis is rejected; otherwise, it is not rejected. Since the t-table or software is required to find the exact P-value and critical t-value, we cannot provide these specific results without such tools.