the equation of the line
 is
is
![\[ x = 2 - 6t, \quad y = 9 - 11t, \quad z = -4 + 12t \]](https://img.qammunity.org/2024/formulas/mathematics/college/8dny1eglwg4ay8len0rw1bpq20e8shq4ge.png) . The coordinates of point (Q) are
. The coordinates of point (Q) are
 . Since
. Since
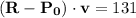 (positive), (R) is on the same side.
(positive), (R) is on the same side.
(a) Equation of the Line:
The equation of the line
 passing through points
passing through points
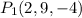 and
and
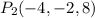 can be represented in vector form as follows:
can be represented in vector form as follows:
![\[ \mathbf{r} = \mathbf{P_1} + t(\mathbf{P_2} - \mathbf{P_1}) \]](https://img.qammunity.org/2024/formulas/mathematics/college/po61j370cme8hpxhzqn01zi85se4mx2qed.png)
Where:
-
 is a vector representing any point on the line,
is a vector representing any point on the line,
-
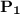 is the position vector of point
is the position vector of point
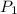 ,
,
-
 is the position vector of point
is the position vector of point
 , and
, and
-
 is a scalar parameter.
is a scalar parameter.
Let's calculate the direction vector
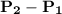 :
:
![\[ \mathbf{P_2} - \mathbf{P_1} = \langle -4 - 2, -2 - 9, 8 - (-4) \rangle = \langle -6, -11, 12 \rangle \]](https://img.qammunity.org/2024/formulas/mathematics/college/t44ddnsjgahkkue0jvle3d7xe5ckbvmor1.png)
Now, the equation of the line is:
![\[ \mathbf{r} = \langle 2, 9, -4 \rangle + t \langle -6, -11, 12 \rangle \]](https://img.qammunity.org/2024/formulas/mathematics/college/m46ikklfuo771wn0ki46c7zqqqudsf9h1c.png)
So, the equation of the line
 is:
is:
![\[ x = 2 - 6t, \quad y = 9 - 11t, \quad z = -4 + 12t \]](https://img.qammunity.org/2024/formulas/mathematics/college/8dny1eglwg4ay8len0rw1bpq20e8shq4ge.png)
(b) Coordinates of Point Q at 40% of the Distance:
To find the point
 at 40% of the distance from
at 40% of the distance from
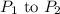 , we can use the parameter
, we can use the parameter
 :
:
![\[ \mathbf{Q} = \mathbf{P_1} + 0.4 (\mathbf{P_2} - \mathbf{P_1}) \]](https://img.qammunity.org/2024/formulas/mathematics/college/xzpj99v2rj7j2toif023jzmo128pa37ruj.png)
Calculate
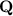 :
:
![\[ \mathbf{Q} = \langle 2, 9, -4 \rangle + 0.4 \langle -6, -11, 12 \rangle \]](https://img.qammunity.org/2024/formulas/mathematics/college/65xqtp9eqnqjnucnz5hqjblw291nr7kd5n.png)
![\[ \mathbf{Q} = \langle 2, 9, -4 \rangle + \langle -2.4, -4.4, 4.8 \rangle \]](https://img.qammunity.org/2024/formulas/mathematics/college/q8i88xzqynnndnhr2cmi4gimdo2bqndc8w.png)
![\[ \mathbf{Q} = \langle -0.4, 4.6, 0.8 \rangle \]](https://img.qammunity.org/2024/formulas/mathematics/college/6iyt0w701ied7przl2cm9pjeke2i2x455x.png)
So, the coordinates of point (Q) are
 .
.
(c) Distance from Point R to the Line:
The distance
 between a point
between a point
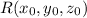 and a line with direction vector
and a line with direction vector
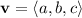 and passing through the point
and passing through the point
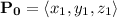 is given by the formula:
is given by the formula:
![\[ d = \frac{\left|(\mathbf{R} - \mathbf{P_0}) \cdot \mathbf{v}\right|}{\|\mathbf{v}\|} \]](https://img.qammunity.org/2024/formulas/mathematics/college/4x8d6azjxoar2q3zhprvqdjdveax3jhy2l.png)
Here,
 represents the dot product, and
represents the dot product, and
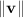 is the magnitude of
is the magnitude of
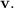
Let
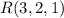 be the point, and
be the point, and
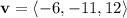 be the direction vector. Also, let
be the direction vector. Also, let
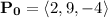 .
.
Calculate the distance:
![\[ \mathbf{R} - \mathbf{P_0} = \langle 3 - 2, 2 - 9, 1 - (-4) \rangle = \langle 1, -7, 5 \rangle \]](https://img.qammunity.org/2024/formulas/mathematics/college/ak1lnrjp6f6jet7gay27r1spyywmn1xrib.png)
![\[ \|\mathbf{v}\| = √((-6)^2 + (-11)^2 + 12^2) = √(36 + 121 + 144) = √(301) \]](https://img.qammunity.org/2024/formulas/mathematics/college/euwuhn1h6clsarrz6fa281p1yxyrmtg5rm.png)
![\[ \left|(\mathbf{R} - \mathbf{P_0}) \cdot \mathbf{v}\right| = | \langle 1, -7, 5 \rangle \cdot \langle -6, -11, 12 \rangle | = |-6 + 77 + 60| = 131 \]](https://img.qammunity.org/2024/formulas/mathematics/college/puxb8w57j2ojorrjlyrpgsu1g54fjogy8c.png)
![\[ d = (131)/(√(301)) \]](https://img.qammunity.org/2024/formulas/mathematics/college/jagkft8t65aaiywepnh9wx27jyhou0anr9.png)
So, the distance (d) is given by
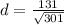 . To determine whether (R) is on the same side or the opposite side of
. To determine whether (R) is on the same side or the opposite side of
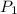 , we can check the sign of
, we can check the sign of
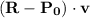 .
.
If it's positive, (R) is on the same side; if negative, it's on the opposite side. In this case, since
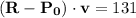 (positive), (R) is on the same side.
(positive), (R) is on the same side.