Question

In a living organism, a fixed fraction 1.30 × 10-12 of 12C is the radioactive isotope 14C, which has a half life of 5730 y.What is the activity of the 14C in 2.4 g of 12C found in living tissue in Bq?

Answer 1

The activity of the
`(^(14)C)` in 2.4 g of
`(^(12)C)` found in living tissue is approximately 6 Bq.

The activity (A) of a radioactive substance can be calculated using the equation:

`A = N \cdot \lambda`

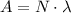
where:

• (N) is the number of radioactive atoms
• 
  `(\lambda)` is the decay constant.

The decay constant is related to the half-life (T) of the substance by the equation:

`$ \lambda = (\ln 2)/(T)`

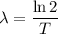
Given that the half-life of
`(^(14)C)` is 5730 years as shown in the question, the decay constant can be calculated by:

`$\lambda = \frac{\ln 2}{5730 , \text{years}} \approx 1.21 * 10^(-4) , \text{year}^(-1)`

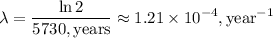
Next, we need to calculate the number of
`(^(14)C)` atoms in 2.4 g of
`(^(12)C)`. This is given by:

`$N_(^(12)C) = \frac{2.4 , \text{g}}{12.01 , \text{g/mol}} * \text{Avogadro number}`

`$N_(^(12)C) = \frac{2.4 , \text{g}}{12.01 , \text{g/mol}} * \ 6.02 * 10^(23)} \approx 1.20 * 10^(23)`

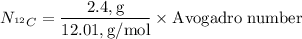
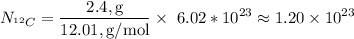
Since the fraction of
`(^(12)C)` that is
`(^(14)C)` is given as
`1.30 * 10^{-12` , the number of
`(^(14)C)` atoms is:

`N_(^(14)C) = 1.20 * 10^(23) * 1.30 * 10^(-12) \approx 1.56 * 10^(11)`

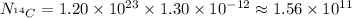
Finally, we can calculate the activity:

`A = N_(^(14)C) \cdot \lambda \approx 1.56 * 10^(11) \cdot 1.21 * 10^(-4) , \text{year}^(-1)`

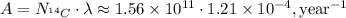
To convert this to Bq (decays per second), we need to multiply by the number of seconds in a year:

`A \approx 1.56 * 10^(11) \cdot 1.21 * 10^(-4) , \text{year}^(-1) * 3.15 * 10^(7) , \text{s/year} \approx 6 , \text{Bq}`

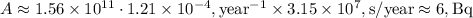
So, the activity of the
`(^(14)C)` in 2.4 g of
`(^(12)C)` found in living tissue is approximately 6 Bq.