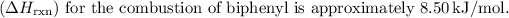The enthalpy change
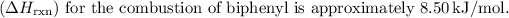
To find the enthalpy change
 for the combustion of biphenyl (
for the combustion of biphenyl (
 ), you can use the equation:
), you can use the equation:
![\[\Delta H_{\text{rxn}} = q_{\text{calorimeter}} = (q)/(n)\]](https://img.qammunity.org/2024/formulas/chemistry/college/k5j5253txespnzk9y67mke8laelf7lhxa0.png)
where:
 is the heat absorbed by the calorimeter,
is the heat absorbed by the calorimeter,
 is the number of moles of biphenyl.
is the number of moles of biphenyl.
First, let's calculate the heat absorbed by the calorimeter
 using the formula:
using the formula:
![\[q_{\text{calorimeter}} = C_{\text{calorimeter}} \cdot \Delta T\]](https://img.qammunity.org/2024/formulas/chemistry/college/xxnnbv9svo2idsxx6qtoo8s253n8je3dtu.png)
where:
 is the heat capacity of the bomb calorimeter,
is the heat capacity of the bomb calorimeter,
 is the temperature change.
is the temperature change.
Given:
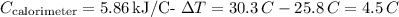
Substitute these values to find \(q_{\text{calorimeter}}\):
![\[q_{\text{calorimeter}} = 5.86 \, \text{kJ/\degree C} * 4.5 \, \degree C = 26.37 \, \text{kJ}\]](https://img.qammunity.org/2024/formulas/chemistry/college/w4p2k9w2tw1yzax8qyl1lc0fl57y2pn3u4.png)
Now, we need to find the number of moles
 of biphenyl. To do this, we can use the molar mass of biphenyl
of biphenyl. To do this, we can use the molar mass of biphenyl
 .
.
![\[\text{Molar mass of } C_(12)H_(10) = (12 * \text{atomic mass of C}) + (10 * \text{atomic mass of H})\]](https://img.qammunity.org/2024/formulas/chemistry/college/u8p5wao3wrqdspdmod0e3jyyzgyqvl7nzx.png)
Using the atomic masses:
- Atomic mass of C ≈ 12.01 g/mol
- Atomic mass of H ≈ 1.01 g/mol
![\[\text{Molar mass of } C_(12)H_(10) = (12 * 12.01) + (10 * 1.01) \, \text{g/mol} = 154.22 \, \text{g/mol}\]](https://img.qammunity.org/2024/formulas/chemistry/college/fh5vb2yqhrjbbpkchnqgv8p5sdauo62cbq.png)
Now, calculate the number of moles
 using the given mass of biphenyl
using the given mass of biphenyl
 :
:
![\[n = \frac{\text{mass}}{\text{molar mass}} = \frac{0.478 \, \text{g}}{154.22 \, \text{g/mol}} \approx 0.0031 \, \text{mol}\]](https://img.qammunity.org/2024/formulas/chemistry/college/ca8q3mux12qjitfl56uy7l72xn4335xnwu.png)
Finally, substitute
 :
:
![\[\Delta H_{\text{rxn}} = \frac{26.37 \, \text{kJ}}{0.0031 \, \text{mol}} \approx 8500 \, \text{kJ/mol}\]](https://img.qammunity.org/2024/formulas/chemistry/college/361r6fg251pufkhh05jo05rba810m3krud.png)
Expressed to three significant figures, the enthalpy change