Question

The height of a substance person jumping off a building that is 20 M high is modeled by the equation 8 equals 20 - 5 t squared.

Answer 1

The substance person's height when jumping off a 20-meter building can be determined using the equation 8 = 20 - 5t², t ≈ ±√(2/5), but since time cannot be negative Then t approximately t ≈ 1.58 seconds.

Step-by-step explanation:

The given equation 8 = 20 - 5t² models the height of the substance person as a function of time (t) when jumping off a 20-meter building. To find the time it takes for the person to reach a height of 8 meters, we need to solve for t. Rearranging the equation:

8 = 20 - 5t²

5t² = 12

`\[ t^2 = (12)/(5) \]`

t ≈ ±
`\sqrt{(12)/(5)} \)`

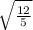
Since time cannot be negative in this context, we discard the negative solution. Therefore, t ≈
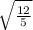`\sqrt{(12)/(5)} \)`, which simplifies to approximately 1.58 seconds.

The solution tells us that the substance person reaches a height of 8 meters after around 1.58 seconds of jumping off the building. This mathematical approach allows us to precisely determine the time at which the specified height is achieved. Understanding such equations is crucial for modeling and predicting physical phenomena in various real-world scenarios.

Full Question:

The height of a substance person jumping off a building that is 20 M high is modeled by the equation 8 = 20 - 5t². Find the t.