Question

Find the domain and range of the following function f(x) = 31x + 71 - 2?

a) Domain: (-[infinity], [infinity]) Range: (-2, [infinity])
b) Domain: (-2, [infinity]) Range: (-800, [infinity])
c) Domain: (-[infinity], -2) Range: (-[infinity], [infinity])
d) Domain: (-[infinity], [infinity]) Range: (-[infinity], -2)

Answer 1

d) Domain:
`(-[infinity], [infinity]) Range: (-[infinity], -2)` the range is (-∞, -2), covering all values below -2 but excluding -2 itself, leading to the final answer of d) Domain: (-∞, ∞) Range: (-∞, -2)."".

Step-by-step explanation:

The function
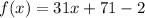`\(f(x) = 31x + 71 - 2\)` is a linear function with a constant slope of 31. In this case, both the domain and range span the entire real number line (-∞, ∞). The domain covers all possible x-values since there are no restrictions on the input values for the function.

For the range, since the function is a linear equation with a positive slope, it continuously increases and extends downward indefinitely. Consequently, the range extends from negative infinity to -2, but it never reaches -2 due to the nature of the function being unbounded in the downward direction. Thus, the correct answer is d) Domain: (-∞, ∞) Range: (-∞, -2).

The function's domain (-∞, ∞) encompasses all real numbers since there are no restrictions on the values of x that can be plugged into the function.

Regarding the range, as the function has a positive slope and an intercept of -2, it continuously increases as x increases, while the output values never reach -2 but get arbitrarily close to it. This behavior results in the range being all values less than -2, extending indefinitely downward but never actually reaching -2. Therefore, the range is (-∞, -2), covering all values below -2 but excluding -2 itself, leading to the final answer of d) Domain: (-∞, ∞) Range: (-∞, -2)."".