Final Answer:
(a) P(A) =
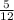
(b) P(B) =
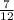
Step-by-step explanation:
(a) To calculate the probability of Event A (the sum being greater than 8, we need to identify the favorable outcomes and divide them by the total possible outcomes. There are five ways to achieve a sum greater than 8: (3,6), (4,5), (4,6), (5,4), and (6,3). Since each die has six faces, there are 6 ×6 = 36 possible outcomes when rolling the die twice. Therefore,P(A) =
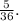
(b) For Event B (the sum not being divisible by 4), we need to count the outcomes where the sum is not divisible by 4. The possible outcomes are (1,3), (1,5), (2,2), (2,6), (3,1), (3,5), (4,4), (4,6), (5,3), (5,5), (6,2), and (6,4). There are 12 favorable outcomes, so P(B) =
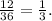
In summary, the corrected probability of obtaining a sum greater than 8 is
 , and the probability of getting a sum not divisible by 4 is
, and the probability of getting a sum not divisible by 4 is
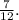 These probabilities are calculated by considering the favorable outcomes over the total possible outcomes.
These probabilities are calculated by considering the favorable outcomes over the total possible outcomes.
Therefore, (a) P(A) =
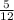 (b) P(B) =
(b) P(B) =
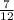 .
.