Question

In a communication system, a 20-bit frame is transmitted, and there exists a bit-error-rate 'p' in the transmission. Calculate the following probabilities:

1. What is the probability that the entire 20-bit frame has no errors during transmission?
2. Determine the probability of a single bit being in error during the transmission process.

Answer 1

1. The probability that the entire 20-bit frame has no errors during transmission is
`(1-p)^2^0.`

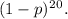
2. The probability of a single bit being in error during the transmission process is
`20 * p * (1-p)^1^9`.

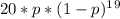Step-by-step explanation:

1. The probability of no errors in a single bit transmission is (1-p). Since there are 20 bits in the frame, the probability of the entire frame being error-free is
`(1-p)^2^0`.

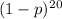2. To find the probability of a single bit being in error during the transmission process, we consider that any one of the 20 bits could be in error. Therefore, we multiply the probability of a single bit being in error (p) by the probability of the remaining 19 bits being error-free
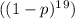`((1-p)^1^9)`. The expression for this is
`20 * p * (1-p)^1^9.`

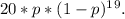
In summary, for the first part, the probability that the entire 20-bit frame has no errors is simply the product of the individual probabilities of each bit being error-free. For the second part, we consider the probability of a single bit being in error and multiply it by the probability of the remaining bits being error-free. These calculations are based on the assumption that errors in different bits are independent events.