Question

Given the equation of the line: 4y - 2x = 16, rewrite it as:

a) m = 2, b = -4
b) m = -2, b = 4
c) m = -4, b = 2
d) m = 4, b = -2

Answer 1

To rewrite the given equation 4y - 2x = 16 in slope-intercept form y = mx + b, the correct values are m = -4 and b = 2, leading to option c as the correct answer. The correct option is c) \( m = -4, b = 2 \).

Step-by-step explanation:

The given equation of the line is in the form 4y - 2x = 16. To rewrite it in slope-intercept form y = mx + b, where m is the slope and b is the y-intercept, we need to isolate y. Starting with the original equation:

4y - 2x = 16

First, add 2x to both sides:

4y = 2x + 16

Now, divide both sides by 4 to solve for y:

`\[ y = (1)/(2)x + 4 \]`

Comparing this with the slope-intercept form y = mx + b, we find that
`\(m = (1)/(2)\) and \(b = 4\)`. However, the options provided are in the form m and b but with opposite signs. To match the options, we need to find their negatives. Therefore,
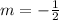`\(m = -(1)/(2)\)` and b = -4, which corresponds to option c: \(m = -4, b = 2\).