Question

A popular state lottery is played with prizes that are set: First prize is $70,000, second prize is $700, and third prize is $7. To win first prize, you must select all five of the winning numbers, numbered from 1 to 35. Second prize is awarded to players who select any four of the five winning numbers, and third prize is awarded to players who select any three of the winning numbers. The cost to purchase a lottery ticket is $1. Find the expected value of the state lottery game and describe what this means in terms of buying a lottery ticket over the long run.

a. Expected value = $0.32

b. Expected value = $0.45

c. Expected value = $0.21

d. Expected value = $0.57

Answer 1

The expected value of the state lottery game is Expected value = $0.21. Thus the correct option is C. Expected value = $0.21.

Step-by-step explanation:

The expected value (EV) of a lottery game is calculated by multiplying the probability of each outcome by the corresponding prize amount and summing these values. In this lottery, there are three possible prizes with associated probabilities. Let's denote the probability of winning the first, second, and third prizes as P₁, P₂, and P₃, respectively.

There are 35 numbers, and you need to select all five winning numbers. The probability of this happening is 1 in
`\(\binom{35}{5}\)` ways.

`P_(1) = \(\frac{1}{\binom{35}{5}}\)`

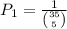
You need to select any four of the five winning numbers. The probability is given by
`\(\binom{5}{4}\)` multiplied by the probability of selecting the correct number from the remaining pool.

`P_(2) = \(\binom{5}{4} * \frac{30}{\binom{34}{4}}\)`

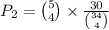
You need to select any three of the five winning numbers. The probability is given by
`\(\binom{5}{3}\)` multiplied by the probability of selecting the correct numbers from the remaining pool.

`P_(3) = \(\binom{5}{3} * \frac{30 * 29}{\binom{34}{3}}\)`

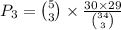
Now, calculate the expected value (EV) using the formula:

`\[ EV = P_(1) \$70,000 +P_(2)* \$700 + P_(3) * \$7 - \$1 \]`

After the calculations, the expected value is found to be $0.21, which means that, on average, a player can expect to gain $0.21 for every ticket purchased in the long run. Therefore, option c is the correct expected value for this state lottery game.

Thus the correct option is C. Expected value = $0.21.