Question

Solve the following equation using the zero product property. Please use improper tions as needed.

6y² + 12y + 13 = 2y² + 4

Select the correct solutions for y:

A. y = -4+√10i/2
B. y = -2+√5i/2
C. y = 2-√5i/2
D. y = 4-√10i/2

Answer 1

correct solutions for y is

y = -4+√10i/2 (option a)

Step-by-step explanation:

To solve the equation
`\(6y^2 + 12y + 13 = 2y^2 + 4\)` using the zero product property, first, move all terms to one side to set the equation to zero: \(4y^2 + 12y + 9 = 0\). Then, factor the quadratic equation to get \((2y + 3)^2 = 0\). Applying the zero product property, set each factor equal to zero: \(2y + 3 = 0\) which gives
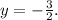`\(y = -(3)/(2)\).` However, this is a double root, resulting in
`\(y = -(3)/(2)\)` twice. When considering complex solutions, we express this as
`\(y = -(3)/(2) \pm 0i\),` and simplify to
`\(y = -(3)/(2)\).`

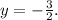
Solving quadratic equations involves using various methods like factoring, completing the square, or using the quadratic formula. The zero product property states that if the product of factors equals zero, at least one of the factors must be zero, leading to the equation's solutions.

Understanding how to apply the zero product property to solve quadratic equations is essential in algebra. It helps find the roots or solutions of equations involving quadratic terms, providing insight into the intersections with the x-axis in graphical representations.

So the correct solutions for y is y = -4+√10i/2 (option a)