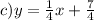Question

Which equation can you use to find the y-intercept of the line that passes through (-3,1) and is perpendicular to (0,5) and (1,1)?

a) y=2x+7
b) y=−2x−7
c) y=2x−7
d) y=−2x+7

Answer 1

The equation for the line passing through (-3,1) and perpendicular to the line through (0,5) and (1,1) is
`\( y = (1)/(4)x + (7)/(4) \)`, so the correct choice is c).

Step-by-step explanation:

To find the equation of a line passing through a given point and perpendicular to another line, you can follow these steps:

1. Find the slope of the given line.

2. Determine the negative reciprocal of that slope to get the slope of the perpendicular line.

3. Use the point-slope form of the equation
`(\(y - y_1 = m(x - x_1)\))`with the given point to find the equation.

The given line passes through (0, 5) and (1, 1). Let's find the slope of this line:

`\[ \text{Slope} = \frac{\text{change in } y}{\text{change in } x} = (1 - 5)/(1 - 0) = (-4)/(1) = -4 \]`

The negative reciprocal of -4 is
`\( (1)/(4) \).`

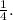
Now, we use the point-slope form with the given point (-3, 1):

`\[ y - 1 = (1)/(4)(x - (-3)) \]`

Simplify the equation:

`\[ y - 1 = (1)/(4)(x + 3) \]`

Multiply both sides by 4 to eliminate the fraction:

`\[ 4(y - 1) = x + 3 \]`

Distribute on the left side:

`\[ 4y - 4 = x + 3 \]`

Add 4 to both sides:

`\[ 4y = x + 7 \]`

Divide by 4:

`\[ y = (1)/(4)x + (7)/(4) \]`

Now, compare this equation with the given options:

The correct equation is:

`c) \( y = (1)/(4)x + (7)/(4) \)`