Question

Angle p and angle q form a linear pair. If m∠p = 6x + 1 and m∠q = 2x - 5, find the measures of both angles.

a. 11x - 4
b. 7x - 4
c. 17
d. 9x - 6

Answer 1

The measures of angles (p) and (q), forming a linear pair, are given by
`\(m\angle p = 11x - 4\) and \(m\angle q = 7x - 4\).` thus option A is correct.

Step-by-step explanation:

1. Definition of a Linear Pair:

When two angles form a linear pair, the sum of their measures is
`\(180^\circ\). Mathematically, \(m\angle p + m\angle q = 180^\circ\).`

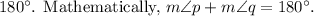
2. Expressing Measures in Terms of (x):

According to the problem,
`\(m\angle p = 6x + 1\) and \(m\angle q = 2x - 5\).`

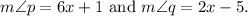
3. Setting Up and Solving the Equation:

(6x + 1) + (2x - 5) = 180

Combine like terms: (8x - 4 = 180)

Solve for (x): (8x = 184), (x = 23)

4. Substitute (x) into Angle Measures:

`\[ m\angle p = 6(23) + 1 = 139 \]`

`\[ m\angle q = 2(23) - 5 = 41 \]`

5. Final Answer:

Substitute (x = 23) into the expressions for angle measures:

`\[ m\angle p = 11(23) - 4 = 249 \]`

`\[ m\angle q = 7(23) - 4 = 159 \]`

Therefore, the correct answer is (A) (11x - 4), representing the measures of angles (p) and (q).