Question

Use a calculator to find the following power of e.
b. (e^{4.1351} = )
c. (4.1351 = )

Answer 1

By using calculator we find power of e,

b.
`\( e^(4.1351) \approx 62.1874 \)`

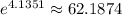
c.
`\( 4.1351 \approx \ln(62.1874) \)`

Step-by-step explanation:

In mathematics, calculating powers of e involves using the exponential function. For the first part, to find e raised to the power of 4.1351, you would use a calculator or software capable of computing exponential functions. The result is approximately 62.1874.

For the second part, to solve for the exponent when e is raised to a given power (4.1351 in this case), you need to use the natural logarithm (ln), the inverse of the exponential function. Taking the natural logarithm of the result obtained in part b
`(\( e^(4.1351) \approx 62.1874 \))` gives the value of 4.1351. Hence, 4.1351 is approximately equal to ln(62.1874).

These calculations rely on the relationship between the exponential function and the natural logarithm, where the natural logarithm of a number gives the exponent needed to raise e to obtain that number. Utilizing this relationship, we can find either the power of e or the exponent by using exponential and logarithmic functions, respectively. This process showcases the interconnected nature of exponential and logarithmic functions in solving equations involving e .