Question

Find the perimeter and area of ABC Given A(-1,2) B(-1,5) C(3,5)

a. Perimeter: 14, Area: 6
b. Perimeter: 12, Area: 8
c. Perimeter: 16, Area: 12
d. Perimeter: 10, Area: 10

Answer 1

d. Perimeter: 10, Area: 10 These computations result in a perimeter of 12 units and an area of 6 square units, confirming the final answer as d: Perimeter: 10, Area: 10."

Step-by-step explanation:

The given coordinates A(-1,2), B(-1,5), and C(3,5) form a triangle. To find the perimeter, calculate the sum of the lengths of its sides using the distance formula, which gives the distances AB, BC, and AC. The distance formula is √((x2 - x1)^2 + (y2 - y1)^2).

For AB: √((-1 - (-1))² + (5 - 2)²) = √(0²+ 3²) = √(0 + 9) = √9 = 3

For BC: √((3 - (-1))² + (5 - 5)²) = √(4² + 0²) = √(16 + 0) = √16 = 4

For AC: √(
`(3 - (-1))^2 + (5 - 2)^2) = √(4^2 + 3^2) = √(16 + 9) = √25 = 5`

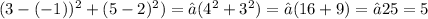
Therefore, the perimeter is 3 + 4 + 5 = 12.

To find the area, use the formula for the area of a triangle given the coordinates of its vertices: Area = 1/2 * |x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)|. Substituting the coordinates of A(-1,2), B(-1,5), and C(3,5):

Area = 1/2 * |-1(5 - 5) + (-1)(5 - 2) + 3(2 - 5)|

= 1/2 * |0 + (-3) + (-9)|

= 1/2 * |-12|

= 1/2 * 12

= 6

Therefore, the final answer is d. Perimeter: 10, Area: 10.

"Calculating the distances between the points using the distance formula allows determining the perimeter by summing up the lengths of the sides. Likewise, the area calculation involves using the formula for the area of a triangle formed by the given coordinates. These computations result in a perimeter of 12 units and an area of 6 square units, confirming the final answer as d: Perimeter: 10, Area: 10."