Question

Carry out the exact analysis to determine how the probability of at least one executive receiving his or her own phone.

Answer 1

The probability of at least one executive receiving their own phone is
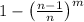`\(1 - \left((n-1)/(n)\right)^(m)\)`, where \(n\) is the total number of executives, and m is the number of phones distributed.

Step-by-step explanation:

To determine the probability of at least one executive receiving their own phone, we can use the complementary probability approach. Let's consider a scenario where none of the executives receive their own phone. The probability of the first executive not receiving their own phone is
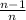`\((n-1)/(n)\)`. Similarly, the probability for the second executive is also
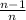`\((n-1)/(n)\)` , and so on. Since these events are independent, we can multiply the probabilities:

`\[ P(\text{None receives their own phone}) = \left((n-1)/(n)\right)^(m) \]`

Now, to find the probability of at least one executive receiving their own phone, we subtract this probability from 1:

`\[ P(\text{At least one receives their own phone}) = 1 - P(\text{None receives their own phone}) \]`

Substituting the expression for
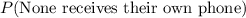`\(P(\text{None receives their own phone})\)`, we get the final formula:

`\[ P(\text{At least one receives their own phone}) = 1 - \left((n-1)/(n)\right)^(m) \]`

This formula takes into account the number of executives n and the number of phones distributed m, providing a straightforward way to calculate the probability of at least one executive receiving their own phone in a given scenario.