Main Answer:
The main answer (y = 2x) reflects the direct variation between (x) and (y), with a constant of proportionality of 2. (b)
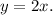
Therefore, the correct answer is b) (y = 2x).
Step-by-step explanation:
In a direct variation, the relationship between two variables, like (x) and (y), is expressed in the form
 is the constant of proportionality. Given the pair of values (x=2) and (y=5), we can substitute these values into the equation and solve for
is the constant of proportionality. Given the pair of values (x=2) and (y=5), we can substitute these values into the equation and solve for
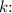
![\[5 = k * 2\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zwdpc3acv19r171qkd7zwtq98ojdyl6qi9.png)
Solving for
 we find that
we find that
 . Substituting \(k\) back into the general equation, we get
. Substituting \(k\) back into the general equation, we get
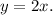 This indicates that the values of (x) and (y) vary directly, with
This indicates that the values of (x) and (y) vary directly, with
 being twice the value of
being twice the value of
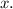 Therefore, option (b)
Therefore, option (b)
 is the correct equation.
is the correct equation.
This equation aligns with the given values, where if
 then
then
 matching the provided (x=2, y=5) pair.
matching the provided (x=2, y=5) pair.
In summary, the correct equation is
 as it accurately represents the direct variation between (x) and (y) with the given pair of values.
as it accurately represents the direct variation between (x) and (y) with the given pair of values.
Therefore, the correct answer is b) (y = 2x).