Question

Example #3: Find the value of x. Then find the measure of each labeled angle.

Answer 1

The value of x is
`\( 30^\circ \)`, and the measure of the labeled angle is
`\( (30-30)^\circ = 0^\circ \)`.

Step-by-step explanation:

The given expression is
`\( (x-30)^\circ \)`. To find the value of x , set the expression equal to zero and solve for x :

`\[ x - 30 = 0 \implies x = 30 \]`

Therefore, x is
`\( 30^\circ \).` Now, substitute this value back into the original expression to find the measure of the labeled angle:

`\[(30-30)^\circ = 0^\circ\]`

So, the final answer is
`\( x = 30^\circ \)` and the labeled angle measures
`\( 0^\circ \)`

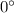
In this context, when x is
`\( 30^\circ \)`, the expression
`\( (x-30)^\circ \)` evaluates to
`\( (30-30)^\circ = 0^\circ \)`. This result makes sense, as subtracting 30 degrees from a value equal to 30 degrees leaves us with zero degrees. The labeled angle, therefore, has a measure of zero degrees. This kind of problem demonstrates the algebraic manipulation of angles, allowing us to find the unknown variable and determine the angle's measure through substitution and simplification.

Full Question:

Example #3: Find the value of x. Then find the measure of each labeled angle.