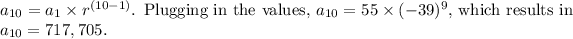Question

Find the 10th term of the geometric sequence. 4) a = -2187 and a₁ = 55​

Answer 1

Finall Answer:

The 10th term of the geometric sequence is 717,705.

Explanation:

To find the 10th term of a geometric sequence, we use the formula
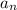`\(a_n`= a_1 \times
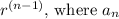`r^((n-1))\), where \(a_n\)` is the nth term,
`\(a_1\)` is the first term, r is the common ratio, and n is the term number. Given that
`\(a_1 = 55\) and \(a = -2187\),`we need to determine the common ratio r.

First, we find the common ratio
`\(r\)`by using the formula
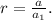`\(r = (a)/(a_1)\).`Substituting the values,
`\(r = (-2187)/(55) = -39\).`

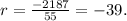
Next, to find the 10th term
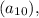`(\(a_(10)\)),` we use the formula
`\(a_(10) = a_1 * r^((10-1))\). Plugging in the values, \(a_(10) = 55 * (-39)^9\), which results in \(a_(10) = 717,705\).`