Question

State the implied domain of f(x)= x-2/x-2 using interval notation.

Answer 1

Main Answer:

The implied domain of
`\(f(x) = (x-2)/(x-2)\)` using interval notation is
`\( \mathbb{R} \setminus \{2\} \).`

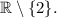
Step-by-step explanation:

In the function
`\(f(x) = (x-2)/(x-2)\),` the expression
`\((x-2)/(x-2)\)` represents the ratio of two identical expressions. However, this ratio is undefined when the denominator is zero. Therefore, the implied domain of the function excludes the value that makes the denominator zero, which is
`\(x = 2\).`

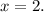
Expressed in interval notation,
`\(\mathbb{R} \setminus \{2\}\)` signifies the set of all real numbers (
`\(\mathbb{R}\))`except for the specific exclusion of 2. This notation elegantly conveys that any real number can be used as an input for
`\(x\)`in the function
`\(f(x)\), except 2.`

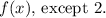
Understanding the implied domain is crucial for avoiding mathematical inconsistencies, as division by zero is undefined. By excluding
`\(x = 2\)`from the domain, we ensure that the function remains well-defined and meaningful for all other real numbers.